A better method for locating sources of gravity and magnetic anomalies

by Leonardo Uieda | 2024/12/20

We have a new preprint out on EarthArXiv which introduces Euler inversion, a new method for finding the location and approximate geometry of sources of gravity and magnetic anomalies.

We’re very excited about Euler inversion because it’s a significant departure from existing methods based on Euler’s homogeneity equation (mainly Euler deconvolution and its many many variants). It’s a brand new mathematical formulation which solves many of the existing issues Euler-based methods, mainly: high sensitivity to noise and interfering sources and the dependence on knowledge of the structural index of the sources. This opens a new research field for us as we continue to improve it further and to explore the capabilities of Euler inversion in difference scenarios!

Open science: As always, all of the source code and data needed to reproduce our results are in the GitHub repository compgeolab/euler-inversion and archived on figshare at doi:10.6084/m9.figshare.26384140. We’ll soon have a version of Euler inversion implemented in the Python library Harmonica as well.

Here’s a sneak peek at our main result from applying Euler inversion to an aeromagnetic dataset from Rio de Janeiro, Brazil:

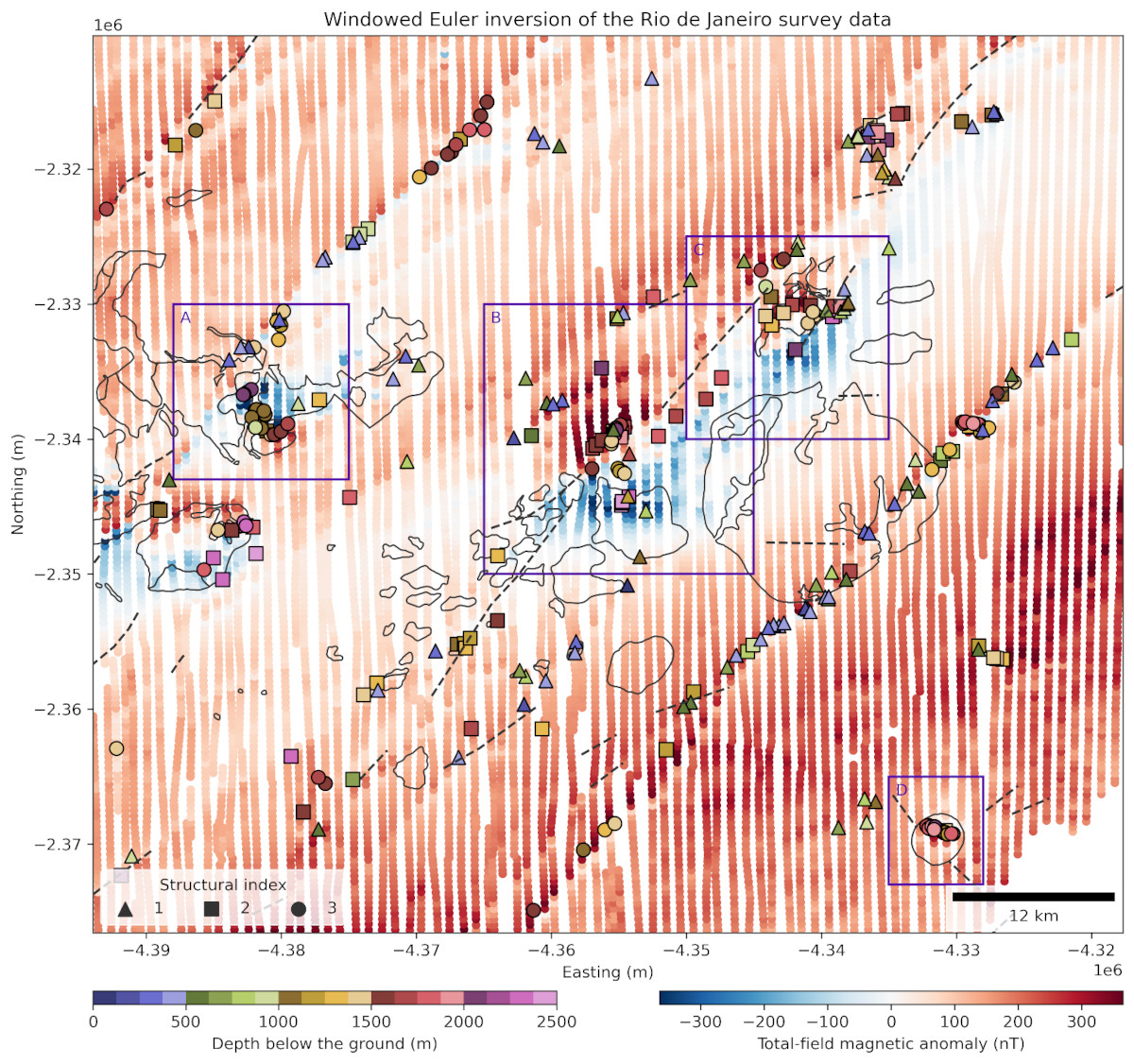
Map with red-white-blue colored dots representing the magnetic anomaly. There are several dipolar looking anomalies and some linear anomalies in the NE-SW direction. Overlaid are small triangles, circles, and squares which follow the dipolar and linear anomalies. — Results of applying Euler inversion with a window size of 12 000 m and a window step of 2400 m to the aeromagnetic data from Rio de Janeiro, Brazil. Estimated source locations and structural indices obtained from Euler inversion are shown as triangles (𝜂 = 1), squares (𝜂 = 2), and circles (𝜂 = 3). The colour of each symbol represents the estimated depth below the surface of the Earth (topography). Also shown are the total-field anomaly flight-line data, the contours of the post-collisional magmatism and alkaline intrusions (solid black lines) and dykes (dashed lines). The purple squares highlight the A, B, C, and D anomalies that are discussed in the text.

The main idea for this paper came about during an potential-field methods class which I took in 2012 with my then PhD supervisor Valéria C. F. Barbosa. While learning about the Euler deconvolution method, which is a speciality of Valéria, I connected it with the geodetic network adjustment theory that I had been taught by Spiros Pagiatakis during an exchange program at York University, Canada, in 2008. An initial prototype was developed in 2012 but there were still some rough edges and the project was shelved to make way for other more urgent projects at the time. I returned to this every few years, making slow progress, and involving Vanderlei C. Oliveira Jr. in the planning and discussion of the theory. In 2024, lab members Gelson and India joined me and Vanderlei for a sprint to finish the method and produce this paper.

Here’s the full reference for the preprint:

Uieda, L., Souza-Junior, G. F., Uppal, I., Oliveira Jr., V. C. (2024). Euler inversion: Locating sources of potential-field data through inversion of Euler’s homogeneity equation. EarthArXiv. doi:10.31223/X5T41M.

We have submitted this to the Geophysical Journal International and are waiting for their reviews. Hopefully everything will work out and we’ll get a nice surprise in the new year when a decision comes back from the editor!

If you have any feedback or would like to use the method, please let us know!

Abstract

Earth scientists can estimate the depth of certain rocks beneath Earth’s surface by measuring the small disturbances that they cause in the Earth’s gravity and magnetic fields. A popular method for this is Euler deconvolution, which is widely available in geoscience software and can be run quickly on a standard computer. Unfortunately, Euler deconvolution has some shortcomings: 1) the approximate shape of the rocks must be known, for example, a sphere or a wide flat slab, represented by the structural index 2) the depth of the rocks is not well estimated when there is noise in our data, which is a common occurrence. We propose a new method, Euler inversion, which fixes some of the shortcomings of Euler deconvolution by using more adequate (and complex) mathematics. Our method is less sensitive to noise in the data and is also able to determine the approximate shape of the source (the structural index). Euler inversion is also fast to execute on a standard computer, making it a practical alternative to Euler deconvolution on an Earth scientists toolbox.

Back to news and lab updates